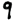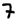
Mean Motion (n_rev):
Two calculate the actual mean motion of the satellite measured in revolutions per day, three values are required. The first two values, the Mean Motion at Epoch n_E and the First Derivative of the Mean Motion MM_dot, are given by the Two Line Elements, while the last value is the Time Since Epoch t_sE.

n_rev = n_E + 2MM_dott_sE

This current Mean Motion n_rev is calculated to take the drag on the satellite into account.

Mean Anomaly (M_t):
The next step is to determine the current Mean Anomaly M_t of the satellites orbital position in degrees. The Mean Anomaly is calculated by using the time since epoch t_sE, the mean anomaly at epoch M_E and the mean motion n_rev at Epoch, both given by the Two Line Elements:

M_t = M_E + 360n_revt_sE

Semi Major Axis (A_km):
The Semi Major Axis A_km, representing the largest radius of an eccentric orbit (in km) as shown earlier, is given by the following equation:

A_km = 331.25e^{[(2/3)log(1440/n_rev)]}

Argument of Perigee (ω) and Right Ascension of Ascending Node (RAAN, Ω):
The Argument of Perigee ω and the Right Ascension of the Ascending Node RAAN are both wandering with a constant speed relative to the ECI coordinate frame. To compensate for this effect in the orbit model, the daily change is determined as ω_dot and RAAN_dot (Both in degrees) in the following two equations. The parameters used here are the orbital Inclination Inc, the orbital Eccentricity ecc (Both found in the Two Line Elements), the Semi Major Axis of the orbit A_km and the Earth's Equatorial Radius r_EarthEq, which is equal to 6378.140km.

ω_dot = [4.98204(r_EarthEq/A_km)^3.5 (5cos(Inc)² - 1)]/[(1-ecc²)²]

RAAN_dot = [9.9641(r_EarthEq/A_km)^3.5 cos(Inc)]/[(1-ecc²)²]

Accordingly the Argument of Perigee ω and Right Ascension of the Ascending Node RAAN are calculated in the following two equations by updating the Argument of Perigee and Right Ascension of the Ascending Node given in the Two Line Elements (ω_TLE and RAAN_TLE).

ω = ω_TLE + ω_dott_sE

RAAN = RAAN_TLE - RAAN_dott_sE